Unidad 2: Sistemas de Numeración y Representación numérica. Aritmética Binaria

Introducción. Los sistemas de numeración y su evolución histórica.
Sistemas de numeración decimal, binario, octal y hexadecimal.
Pasajes entre sistemas de números enteros y positivos.
Representación de Números signados: Convenio de signo y magnitud.
Convenio de complemento a uno. Convenio de complemento a dos.

Unidad 2: Sistemas de Numeración y Representación numérica. Aritmética Binaria

Operaciones de adición y de sustracción utilizando el convenio de complemento a dos.
Representación de números fraccionales. Notación punto fijo y punto flotante. Precisión y truncado. Errores en notación de punto flotante.
Formato IEEE 754.
Representación de caracteres: Binario Codificado Decimal (BCD), ASCII, EBCDIC, Unicode.

Video OnLine

Sistema Binario ¿Cómo es?

Bit, Nibble y Byte

BIT = 0 o 1
nibble = 4 bits
- Intel 4004 : 1971, 2'250 Transistores
Bytes = 8 bits
- Intel 8008 : 1972, 3'500 Transistores
- Intel 8088 : 1979, 29'000 Transistores

Cantidad de bits:

1 bit => 2 símbolos (2ⁿ c/ n=1 => 2)
2 bits => 4 símbolos (2ⁿ c/ n=2 => 4)
3 bits => 8 símbolos (2ⁿ c/ n=3 => 8)
4 bits = nibble => 16 símbolos (2ⁿ c/ n=4 => 16)
8 bits = byte => 256 símbolos (2ⁿ c/ n=8 => 256)

Tamaño de la memoria (en Bytes)

KiloByte = 1KB = 1024 bytes (10³)
MegaByte = 1MB = 1024 KB (10⁶)
GigaByte = 1GB = 1024 MB (10⁹)
TeraByte = 1TB = 1024 GB (10¹²)
PetaByte = 1PB = 1024 TB (10¹⁵)
y siguen Exa, Zetta y Yotta.

Nota: Acá hablamos de Bytes, pero también estas unidades pueden ser en bits. Normalmente se usa la "B" mayúscula para bytes y la "b" minúscula para bits. Por ejemplo cuando se habla de velocidad de transmisión se suelen usar MegaBits.

Representación / Interpretación

hexa, binario, ASCII

Distintos significado de "hecho":

El hecho sucedió en casa
He hecho esto miles de veces

Distintos significado de "visto":

Lo he visto seguido a Juan
Visto y considerando los sucedido...

Disfrutemos mientras podamos...

Representación / Interpretación

Sistemas de Numeración

Dos tipos:
- No posicionales:
- Posicionales:

Bases:
- Decimal: Base 10 (Mano)
- Duodecimal: Base 12 (Meses año)

Computadora: Binaria!
- Base 2 (binario)
- Base 8 (octal)
- Base 16 (hexadecimal)

Duodecimal o Sexagecimal (Sumerio)

Bases binarias

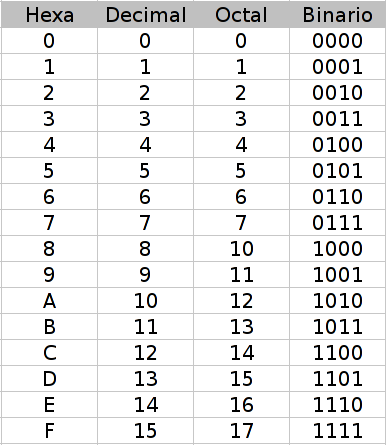
Bit mas y menos significativo

Conversión Decimal a Binario

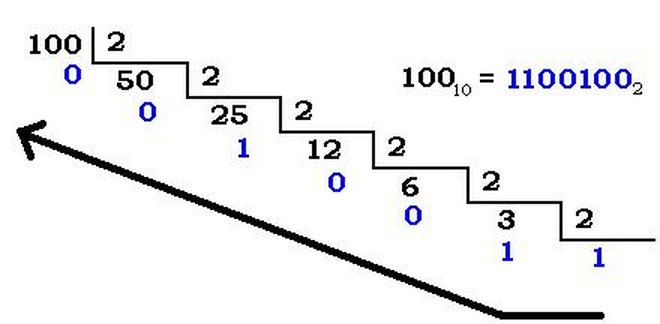
Conversión Binario a Decimal

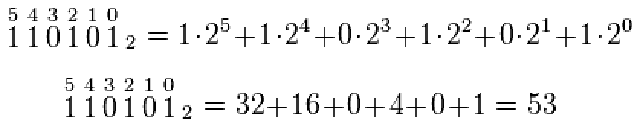
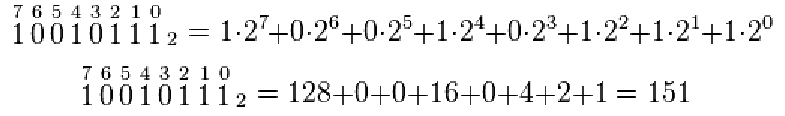
Ejemplo de cálculo por pesos en una hoja de calculos.

Imprimiendo en distintos formatos


#include <stdio.h>

int main(void) {
	int numero = 0;

	printf("Ejemplo: Conversión a octal/hexadecimal/ascii \n");
	printf("Ingrese el numero a convertir \n");
	scanf("%d", &numero);

	printf("Dec: %d - Oct: %o - Hex: %x - Ascii: %c \n", \
		numero, numero, numero, numero);

	return 0;
}

Compilemos y corramos el programa


$ gcc -o conv conversion.c
$ ./conv

Códigos

Binario codificado en decimal (BCD)

Back to the future

Tomorrowland

Binario codificado en decimal (BCD)

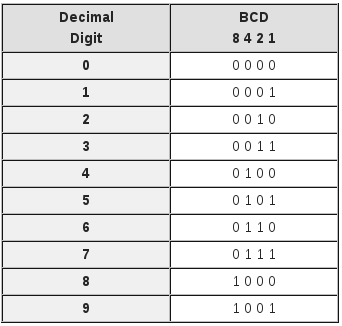
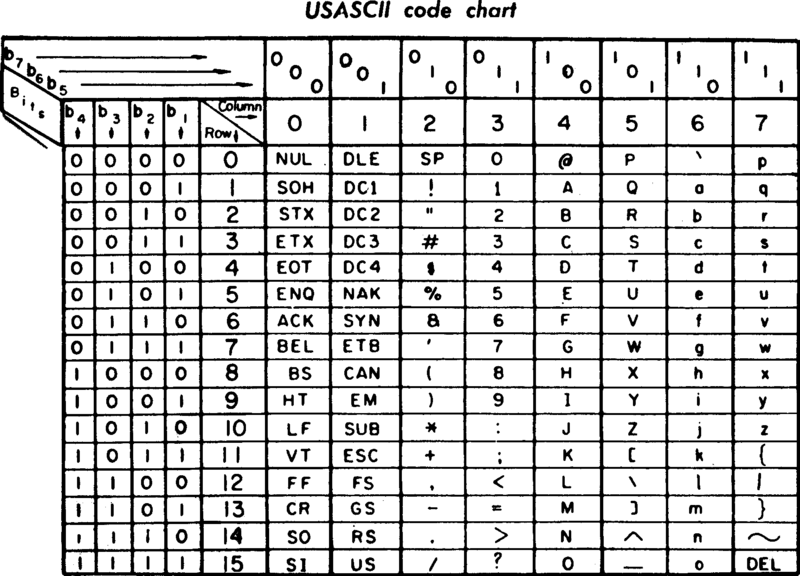
Tabla ASCII

(American Standard Code for Information Interchange)

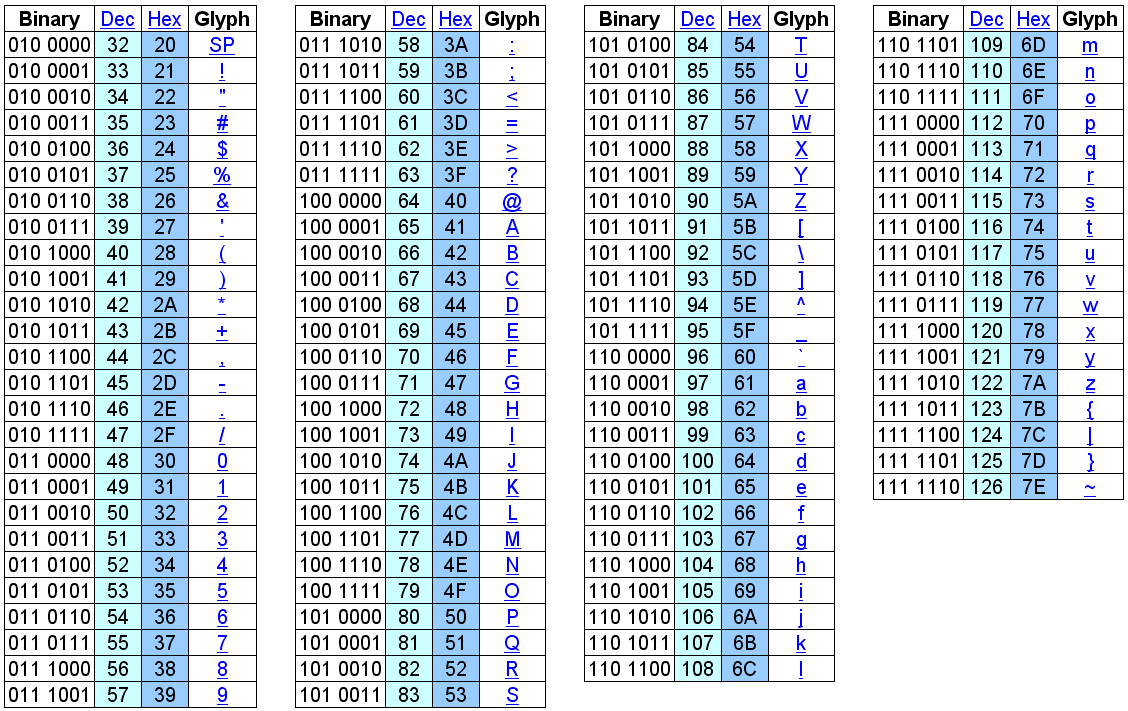
Tabla ASCII con los caracteres no imprimibles

Operaciones Binarias

Distintas formas de llamarlo, pero siempre se refieren a operaciones lógicas

NOT o Negación

Verdadero (negado) = Falso ( !1 = 0 )
Falso (negado) = Verdadero ( !0 = 1 )

Operadores lógicos

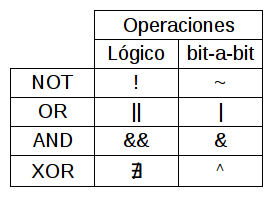
Nota: Al símbolo ˜ se lo denomina Virgulilla o tilde (del ingles). Para el profe es y será un ñuflo.

Multiplicación Lógica (AND &)

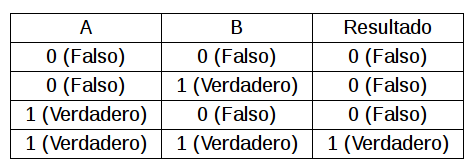
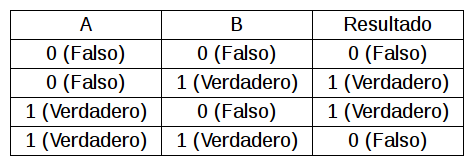
Suma Lógica (OR |)

Suma Exclusiva (XOR ^)

Mas sobre el tema:

Números negativos y fraccionales

(opcional)

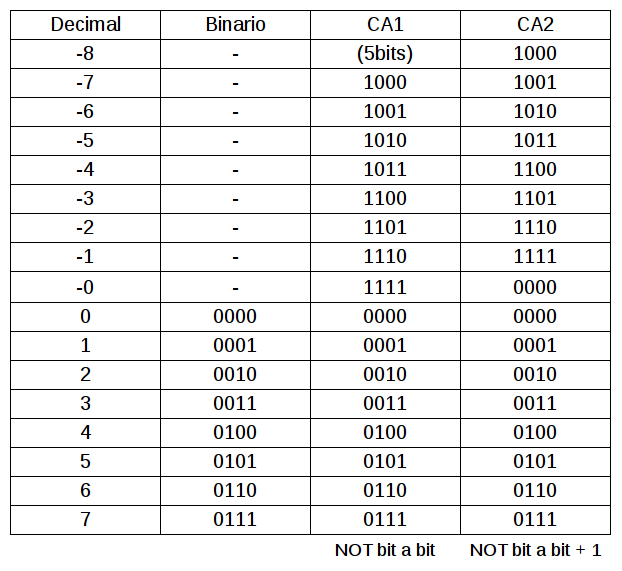
Complemento a 2 (CA2)

Es una forma de representar números negativos

Complemento a 1 (CA1):
- Tiene una doble representación del cero

Complemento a 2 (CA2):
- Mejor rango ( 0 = -0 )

Complemento a 2 (CA2)

Usando CA2 en C

Tipos de datos

char : 8bits
int : 16bits
long : 32bits

Números fraccionales en binario

Representar números fraccionales en binario puede llevar a errores de conversión.

No todos los números fraccionales son representables sin error en binario

Todo número fraccional representado en binario será multiplo de 1/2^x

Números fraccionales en binario

0,1 decimal a bin

0,1 * 2 = 0,2 => 0
0,2 * 2 = 0,4 => 0
0,4 * 2 = 0,8 => 0
0,8 * 2 = 1,6 => 1
0,6 * 2 = 1,2 => 1
sigue...

De acá en mas se repiten las cuatro cifras periódicamente...

0,2 * 2 = 0,4 => 0
0,4 * 2 = 0,8 => 0
0,8 * 2 = 1,6 => 1
0,6 * 2 = 1,2 => 1
...

En orden:

00110011

bin: 0,0011 0011...

Números fraccionales en binario

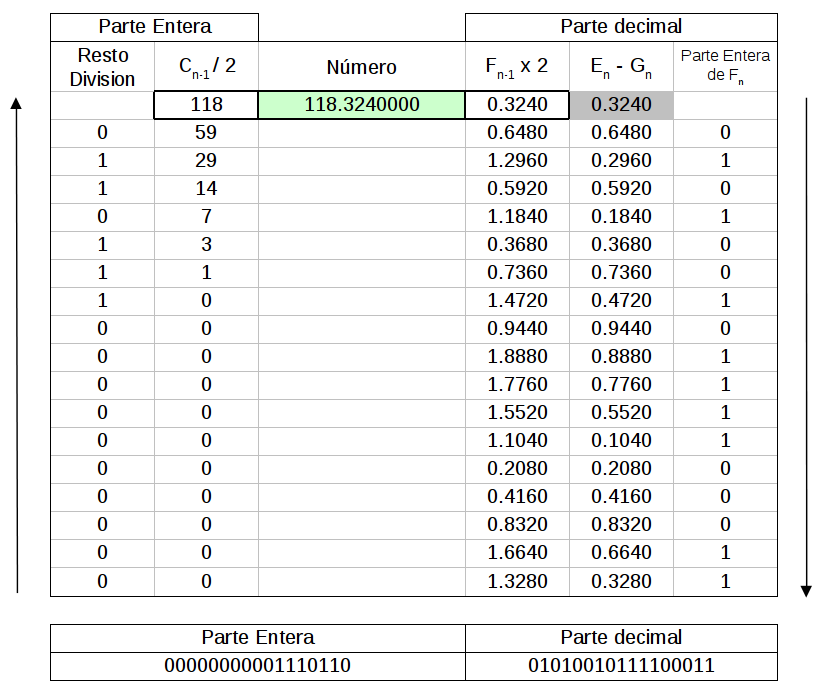
Números fraccionales: Calculadora

Se puede ver con la calculadora que ciertos números fráccionarios pierden precisión al pasarlos de decimal a binario (p/ej 6.1)

Para que el número no pierda precisión su parte decimal debe ser múltiplo de 1/2ⁿ

IEEE 754

(informativo)

Números con coma...

Racionales: Números que pueden representarse como el cociente de dos números enteros (es decir una fracción común)
- 3/4 = 0,75
- 8/5 = 1,6
Periódicos: Es un número racional con parte fraccionaria caracterizado por tener un período (cifras que se repiten infinitamente) en su expansión decimal.
- 2/3 = 0,6666666...
- 1/9 = 0,1111111...
Irracionales: Es un número que no puede ser expresado como una fracción.
- Pi = 3,14159...
- e = 2,7182...

Cáculos en los microcontroladores

Enteros: Se realizan en la unidad aritmético lógica (ej. 8086) que permite sumar, restar, multiplicar, dividir, realizar operaciones binarias, etc... (el acrónimo ALU viene del inglés: Aritmetic Logic Unit).

Fraccionarias: Se pueden realizar por software (lento) o utilizar una unidad funto flotante (ej. 8087) y permite realizar las cuentas matemáticas que hace una calculadora (también denominada FPU del inglés Floting Point Unit).

Formato punto flotante (IEEE 754)

El estándar de la IEEE para aritmética en coma flotante (IEEE 754) es el estándar más ampliamente usado para las computaciones en punto flotante, y es seguida por muchas de las implementaciones de CPU y FPU.

El estándar define formatos para la representación de números en punto flotante (incluyendo el cero) y valores desnormalizados, así como valores especiales como infinito y NaNs conjuntamente con un conjunto de operaciones en punto flotante que opera sobre estos valores.

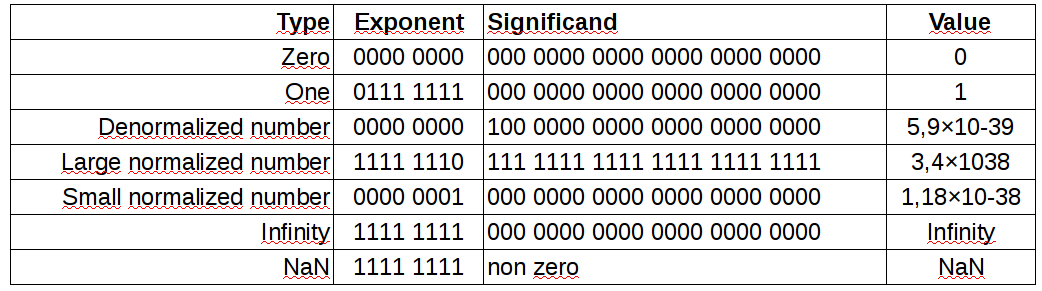
Formato punto flotante (IEEE 754)

Formatos mas usados:
- Mas comunmente implementados (del estándar original IEEE 754-1985):
  - precisión simple o binary32 (32 bits) - float
  - precisión doble o binary64 (64 bits) - double
- Otros formatos aparecidos luego (ultima versión IEEE 754-2008):
  - binary16, binary128, binary256, decimal32, decimal64 y decimal128.

Mas sobre el tema:

Articulo sobre IEEE754 en wikipedia

Formato punto flotante (IEEE 754)

precisión simple (32 bits)

 1     8               23              tamaño en bits
 +-+--------+-----------------------+
 |S|  Exp   |  Fracción             |
 +-+--------+-----------------------+
 31 30    23 22                    0    índice del bit (0 a la derecha)
    desplazado +127

precisión doble (64 bits)

 1     11                                52
 +-+-----------+----------------------------------------------------+
 |S|  Exp      |  Fracción                                          |
 +-+-----------+----------------------------------------------------+
 63 62       52 51                                                 0
    desplazado +1023

IEEE 754

IEEE 754: Ejemplo

Número decimal -118,625

Necesitamos obtener:
- El signo
- El exponente
- La fracción

Dado que es un número negativo, el signo es "1"

Escribimos el número (sin signo) en binario = 1110110,101

IEEE 754: Ejemplo

Número decimal -118,625 - Fracción (normalizada)

Ahora, movamos el punto decimal a la izquierda, dejando solo un 1 a su izquierda:
- 1110110,101 = 1,110110101 x 2⁶
- Esto es un número en coma flotante normalizado

La fracción es la parte a la derecha del punto decimal, rellenada con ceros a la derecha hasta que obtengamos todos los 23 bits:
- 11011010100000000000000

IEEE 754: Ejemplo

Número decimal -118,625 - El Exponente

El exponente es 6, pero necesitamos convertirlo a binario y desplazarlo:
- Para el formato IEEE 754 de 32 bits, el desplazamiento es 127, así es que 6 + 127 = 133.
- En binario, esto se escribe como 10000101.

Por lo tanto la cadena de unos y ceros resultante es:

 +-+--------+-----------------------+
 |S|  Exp   |  Fracción             |
 +-+--------+-----------------------+
 |1|10000101|11011010100000000000000|
 +-+--------+-----------------------+
 31 30    23 22                    0    índice del bit (0 a la derecha)

¿Solo se usa IEEE 754?

Un ejemplo moderno de otros usos lo podemos
encontrar en la Inteligencia Artificial.

Las neuronas artificiales tienen fuertes beneficios de velocidad gracias al uso de números flotantes más pequeños.

FP16 : 1 bit para el signo, 5 bits de exponente y 10 bits de significando.
FP8 : No hay estándard, pero un ejemplo es 1 bit para el signo, 4 para el exponente y 3 para el significando.

Artículo IEEE: The Secret to Nvidia’s AI Success.